Leggendo qua e là su Facebook mi imbatto in Massimo che scrive: Il mio sogno? Far incrociare due rette parallele. Qualsiasi cosa questo significhi.
Poi spiega: È che al lavoro, in amore, e in tante altre cose mi ritrovo con persone che sembrano rette parallele. Spesso il loro atteggiamento è del tipo “siamo due rette parallele, non ci incontreremo mai”. Ma secondo me non è vero…..
Gli dico: Semplice! Basta che abbandoni Euclide e il gioco è fatto.
Credo che sia necessaria una breve spiegazione. Fin dalle elementari ci insegnano che due rette parallele non si incontrano mai. Questo però presuppone un’ipotesi implicita. E cioè che queste linee infinite si muovano su piani -altrettanto infiniti- perfettamente piatti.
Mentre l’infinitezza è un’estrapolazione, la geometria intrinseca del piano -la piattezza- è un’ipotesi, derivante da una struttura mentale che ci siamo dati. Certo, molto ragionevole, ma pur sempre un’ipotesi aggiuntiva.
Ragionevole perché la nostra immediata percezione ci suggerisce questo. E siccome è anche la geometria che permette di semplificare il calcoli, la cosa più sensata da fare per costruire una geometria adeguata a descrivere il nostro mondo pare essere l’assumere i piani piatti. Tutta la dinamica newtoniana è costruita in questa maniera. Ma è ad Euclide (323-286 a.C.) che dobbiamo la formulazione di questa geometria.
Euclide nel suo famoso V Postulato (postulato significa “affermazione non verificabile”) sostiene che per un punto si può condurre una ed una sola retta parallela ad una data retta (che non passa per quel punto, ovviamente).
Ma cosa sono due rette parallele?
Sono due rette che, intersecate da una retta perpendicolare ad una di esse, questa sarà perpendicolare anche all’altra*. Vedi Immagine.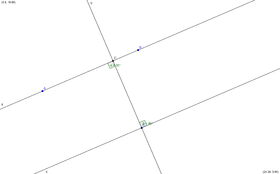
E’ chiaro che se sono su un piano piatto queste non si incontreranno mai.
Ma immaginate i loro percorsi paralleli, invece che sul piano, su una sfera. Oppure su un bizzarro iperboloide. Queste rette parallele potranno incontrarsi se la geometria su cui sono costrette a propagarsi le avvicinerà*.
In questo caso avremo rinunciato ad una delle ipotesi implicite di Euclide, la piattezza dello spazio. Avremo rinunciato al V Postulato e saremo entrati nel mondo delle geometrie non-euclidee.
Se la cosa vi pare bizzarra oppure puramente speculativa, in realtà esse sono più concrete di quanto possa sembrare. E’ stato Einstein a ipotizzare che la geometria del nostro universo sia modificata dalla presenza di masse. Masse grandi equivalgono a grandi deformazioni dalla piattezza, e viceversa. Tutta la Relatività generale deriva da quest’ipotesi (poi confermata sperimentalmente!).
Einstein ha fatto grande uso della geometria non-euclidea sviluppata nel XIX secolo, tra gli altri, dal lughese Gregorio Ricci Curbastro.

Ma non dovete pensare che queste siano cose esotiche rispetto alla nostra vita quotidiana. Immaginiamo due persone all’equatore. Se entrambe iniziano a muoversi verso Nord, secondo voi cosa accade? Esse si muovono su linee sempre parallele tra loro (dette meridiani), ma queste linee, per la curvatura del nostro pianeta, si incontreranno al Polo Nord. Solo che questa curvatura, per gli spostamenti piccoli, quelli di tutti i giorni, è trascurabile. E non c’è bisogno di far ricorso alla geometria non-euclidea su uno sferoide (il nostro pianeta) per descrivere gli spostamenti che facciamo nella vita di tutti i giorni.
Tornando a Massimo, per far sì che due rette parallele si incontrino non occorre far altro che allentare un pochino le nostre pretese.
Dobbiamo essere disponibili a cambiare lo schema in cui si collocano le nostre coordinate, o le nostre certezze.
E anche le rette parallele possono incontrarsi.
Solo i punti, per quanti vicini, non si incontrano mai.
E anche questa mi pare una buona metafora della vita.
Finché c’è retta c’è speranza.
* Prima che i puristi mi sbranino, questa non è la definizione di parallelismo. Ma solo un modo intuitivo per ricordare a chi potrebbe esserselo scordato uno dei teoremi riguardanti le rette parallele nelle geometrie euclidee.
**Attenzione! A volte la geometria può anche allontanare….